Heap?
완전이진트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조
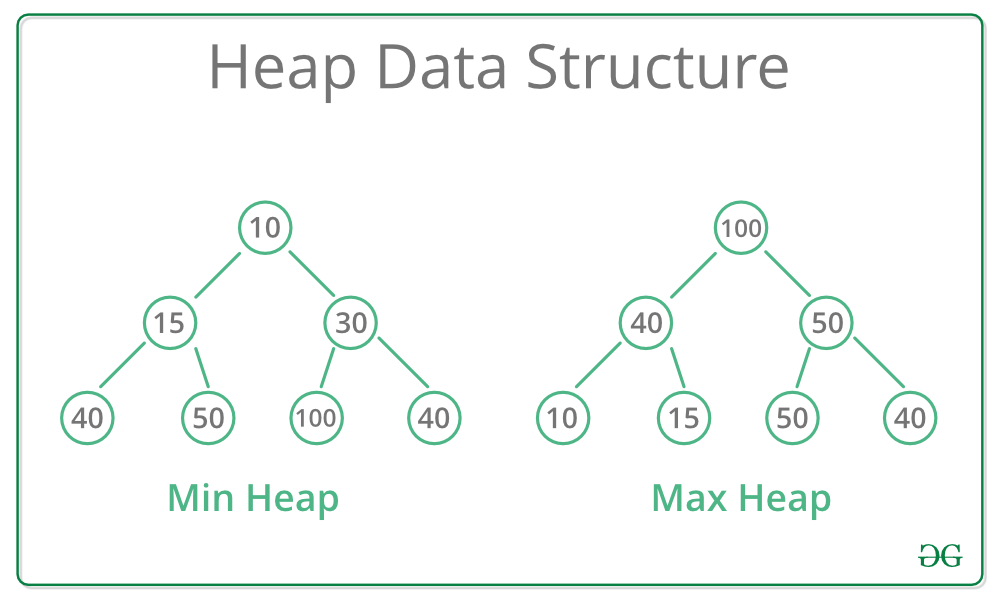
최대 힙(max heap)
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
- 부모 노드의 키 값 > 자식 노드의 키 값
- 루트 노드 : 키 값이 가장 큰 노드
최소 힙(min heap)
- 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
- 부모 노드의 키 값 < 자식 노드의 키 값
- 루트 노드 : 키 값이 가장 작은 노드
Heap에서의 삽입과 삭제
- 삽입 -
- 새 원소를 저장할 수 있도록 힙의 크기를 1만큼 늘린다.
- 힙 끝에 새 요소를 삽입한다.
- 새로 삽입된 원소를 힙의 성격에 맞게 재정렬한다.
최대 힙:
10
/ \
5 3
/ \
2 4
15를 새로 삽입하려고 한다.
Process:
Step 1: 끝에 새 원소를 삽입.
10
/ \
5 3
/ \ /
2 4 15
Step 2: bottom-up 방식으로 힙을 정렬하자.
-> 15가 3보다 크니까 서로 자리 바꿈.
10
/ \
5 15
/ \ /
2 4 3
-> 15가 10보다 크니까 서로 자리 바꿈.
15
/ \
5 10
/ \ /
2 4 3
최종적으로 힙은 다음의 형태를 띄게 된다:
15
/ \
5 10
/ \ /
2 4 3
- 삭제 -
- 삭제할 루트, 요소를 마지막 요소로 바꾼다.
- 힙에서 마지막 요소를 삭제한다.
- 힙의 성격에 맞게 재정렬한다.
Max-Heap:.
10
/ \
5 3
/ \
2 4
루트(10)을 삭제하려고 한다.
1: 마지막 요소(4)를 루트로 교체하고 삭제한다.
4
/ \
5 3
/
2
2: 힙을 재정렬하자.
최종 힙 :
5
/ \
4 3
/
2 이때 삭제에서 주의해야할 것은 힙에서는 루트 노드의 원소만을 삭제할 수 있다는 것이다.
따라서 루트 노드의 원소를 삭제하여 반환한다. 힙의 종류에 따라 최대값 또는 최소값을 구할 수 있다.
'CS > data structure' 카테고리의 다른 글
| Priority Queue (우선순위 큐) (0) | 2021.06.11 |
|---|---|
| 이진탐색트리(Binary Search Tree) (0) | 2021.06.09 |
| Tree (트리) - 2 (0) | 2021.06.07 |
| Tree (트리) - 1 (0) | 2021.06.06 |
| List 리스트 (0) | 2021.03.27 |