선형 자료구조
- 1:1의 관계를 표현한다.
- 한 줄로 줄세울 수 있다.
비선형 자료구조
- 1:1 아닌 관계 1대다 다대다
- ex) 계층적 트리, 그래프 트리는 넓은 의미에서 그래프의 특별한 형태다
Graph?
그래프는 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현한다.
정점(Vertex): 그래프의 구성 요소로 하나의 연결점 - 트리에서의 node
간선(Edge): 두 정점을 연결하는 선
차수(Degree): 정점에 연결된 간선의 수
그래프는 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
* V: 정점의 개수, E: 그래프에 포함된 간선의 개수
* V개의 정점을 가지는 그래프는 최대 V*(V-1)/2 간선이 가능 => 무향그래프일 경우
예) 5개의 정점이 있는 그래프의 최대 간선 수는 10(=>5*4/2)개이다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 N:M관계를 가지는 원소들을 표현하기 용이하다.
그래프 유형

무향 그래프(Undirected Graph) 방향이 없음 -> 서로가 서로를 인지하는 양방향 그래프이다.
유향 그래프(Directed Graph) 방향이 있음 -> 단방향 그래프
가중치 그래프(Weighted Graph)

사이클 없는 방향 그래프(DAG, Directed Acyclic Graph)
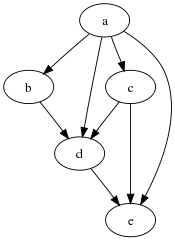
사이클: 정점을 2번 방문하는 그래프
사이클 그래프를 얘기할 때는 무향을 얘기한다.
완전 그래프: 정점들에 대해 가능한 모든 간선들을 가진 그래프
v개 정점이 있는데 모든 정점마다 v-1개 간선을 갖는 그래프
부분 그래프: 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
트리는 싸이클이 없는 무향 연결 그래프이다.
- 두 노드 사이에는 유일한 경로가 존재한다.
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
인접(Adjacency)
두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
완전 그래프에 속한 임의의 두 정점들은 모두 인접해 있다.
그래프에서의 경로란?
경로(Path)란 어떤 정점(A)에서 시작하여 다른 정점(B)로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열한 것
경로 중 한 정점을 최대 한번만 지나는 경로를 단순경로라고 한다.
순환경로란?(Cyclic Path)
- 경로의 시작점과 끝점이 같다
- 경로에서 어떤 정점을 2번이상 거치는 경우이다.
- 1-3-5-1 이렇게 되는 것이다.
그래프를 표현하는 방식
인접 행렬(Adjacent matrix)-> 정점 중심으로 표현할 때 유리하다.
- V x V 크기의 2차원 배열을 이용해서 간선 정보를 저장한다.
- 배열의 배열(Reference Array)
인접 리스트(Adjacent List)-> 정점 중심으로 표현할 때 유리하다.
- 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장한다.
간선 리스트(Edge List)-> 간선 중심으로 표현할 때 유리하다.
- 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장한다.
'CS > data structure' 카테고리의 다른 글
| Tree (트리) - 1 (0) | 2021.06.06 |
|---|---|
| List 리스트 (0) | 2021.03.27 |
| 리스트(list) (0) | 2021.02.12 |
| 큐 (Queue) (0) | 2021.02.11 |
| 스택(Stack) (0) | 2021.02.11 |