* Counting Sort?
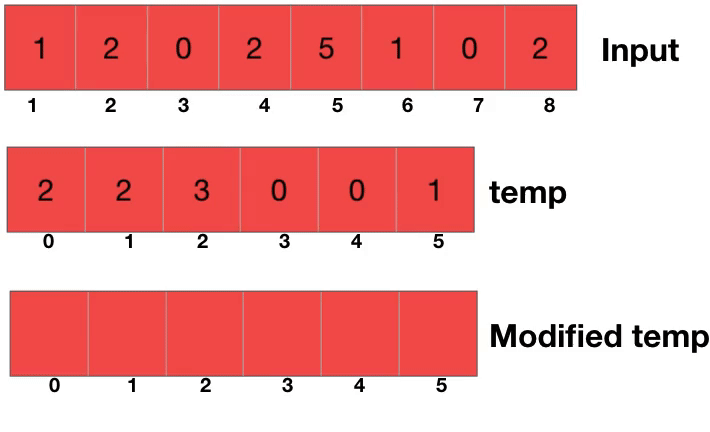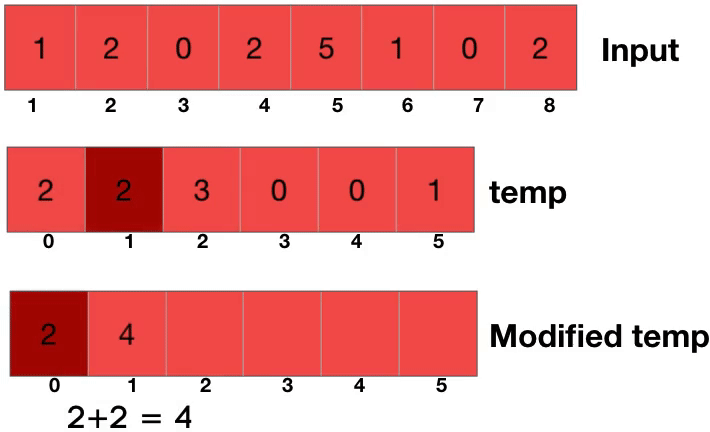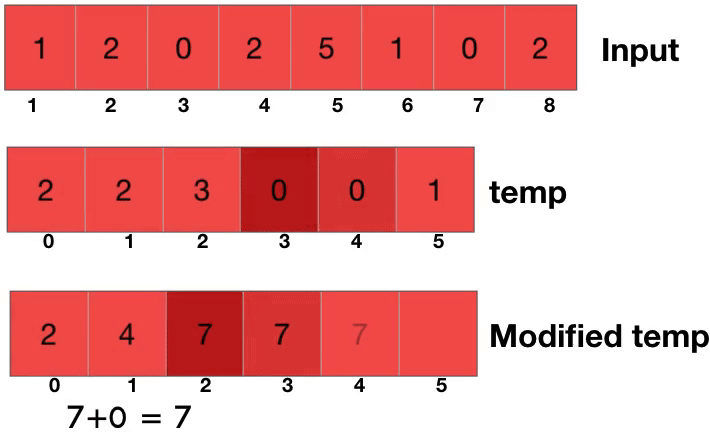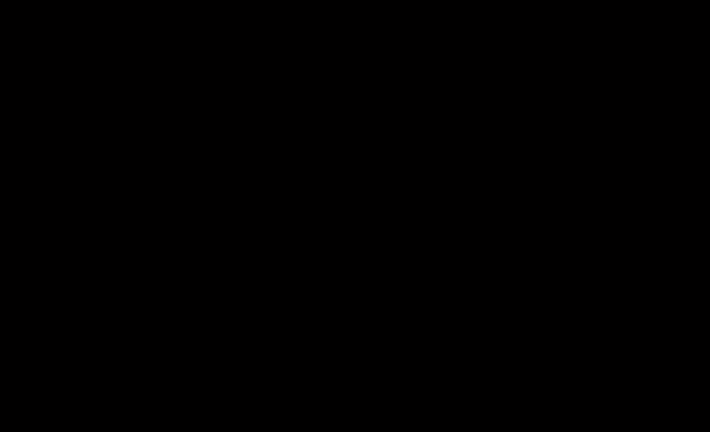
카운팅 소트는 일단 한 수가 몇번 등장하는지를 세는 것에서부터 시작을 한다. 그런다음 누적합을 구해준다. 이게 무슨 소리냐면 0번이 2번, 1번이 2번 나왔다면 누적합 배열에서는 2번 나온 0이 2, 그 다음인 1이 2+2해서 4가 된다는 얘기다. 카운팅 소트의 핵심은 앞의 놈이 몇번 나왔는지 안다면 나는 몇번부터 몇번 인덱스에 걸쳐있을지를 계산할 수 있다는 것이다.
* Pseudocode
CountingSort(A)
//A[]-- Initial Array to Sort
//Complexity: O(k)
for i = 0 to k do
c[i] = 0
//Storing Count of each element
//Complexity: O(n)
for j = 0 to n do
c[A[j]] = c[A[j]] + 1
// Change C[i] such that it contains actual
//position of these elements in output array
////Complexity: O(k)
for i = 1 to k do
c[i] = c[i] + c[i-1]
//Build Output array from C[i]
//Complexity: O(n)
for j = n-1 downto 0 do
B[ c[A[j]]-1 ] = A[j]
c[A[j]] = c[A[j]] - 1
end func출처: www.codingeek.com/algorithms/counting-sort-explanation-pseudocode-and-implementation/
Counting Sort Explanation, Pseudocode, Implementation in C Java | Codingeek
Counting Sort is a linear sorting algorithm with asymptotic complexity O(n+k). In this post we will discuss the counting sort algorithm with pseudocode, implementation in C Java
www.codingeek.com
* 분석
카운팅소트의 시간복잡도는 O(n)으로 굉장히 빠르다는 장점이 있다. 그러나 치명적인 단점이 있는데, 메모리 낭비가 심각할 수 있다는 결함이 있다. 계수정렬은 정렬하려는 값의 최댓값만큼 메모리를 필요로 한다. 예를 들어 1, 2, 3, 1000인 배열을 정렬해야 한다고 하면 임시 배열은 0, 1, 1, (어저구저저구 인덱스 1000까지 감)1이 되며 완성된 누적합의 배열은 0, 1, 2, 3, 3, 3, 3, 3, 3,(어저구저저구 인덱스 1000까지 감)4가 될 것이다. 그러니까 쓰지도 않은 990여개의 배열인덱스때문에 메모리의 낭비가 극심하다. 따라서 정렬할 값들이 특정한 범위에 있을 때에 유리하다. 1~10까지라던가 어떤 좁은 범위에 있어야 메모리 낭비가 적을 것이다. 위의 예시처럼 1,2, 10000000인 수를 정렬해야 할 때에는 그냥 퀵 소트를 쓰자!
'CS > algorithm' 카테고리의 다른 글
| Union-Find Algorithm (0) | 2021.04.14 |
|---|---|
| Dijkstra Algorithm: 다익스트라 알고리즘 (0) | 2021.03.24 |
| Quick Sort: 퀵 정렬 (0) | 2021.03.07 |
| Merge Sort: 합병 정렬 (0) | 2021.03.07 |
| Shell Sort: 쉘 정렬 (0) | 2021.03.07 |