이걸 카테고리를 알고리즘으로 해야하는지... 자료구조로 해야하는지...
* Union-Find (= disjoint-set / merge-find) 알고리즘
Union-Find 알고리즘은 2개의 기능을 가지고 있는 알고리즘이다.
1. Find : 어느 부분집합에 특정한 원소가 있는지를 찾는다. 이것은 두 원소가 같은 부분집합에 포함되어 있는지 찾는 방식으로 사용할 수 있다.
2. Union : 두 부분집합을 하나의 부분집합으로 합친다.
한국말로는 서로소 집합/상호 배타 집합이라고도 불린다.
- 서로소 또는 상호배타 집합들은 서로 중복 포함된 원소가 없는 집합들이다. 교집합이 없다는 소리이다.
- 집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분한다. 구분할 수 있는 이 원소를 대표자(representative)라 한다.
- union-find 를 표현하는 방법
1. 연결리스트

노드 관리를 해야하기 때문에 까다롭다.
2. 트리
하나의 집합(disjoint set)을 하나의 트리로 표현한다.
자식 노드가 부모 노드를 가리키며 루트 노드가 대표자가 된다.
* 문제점
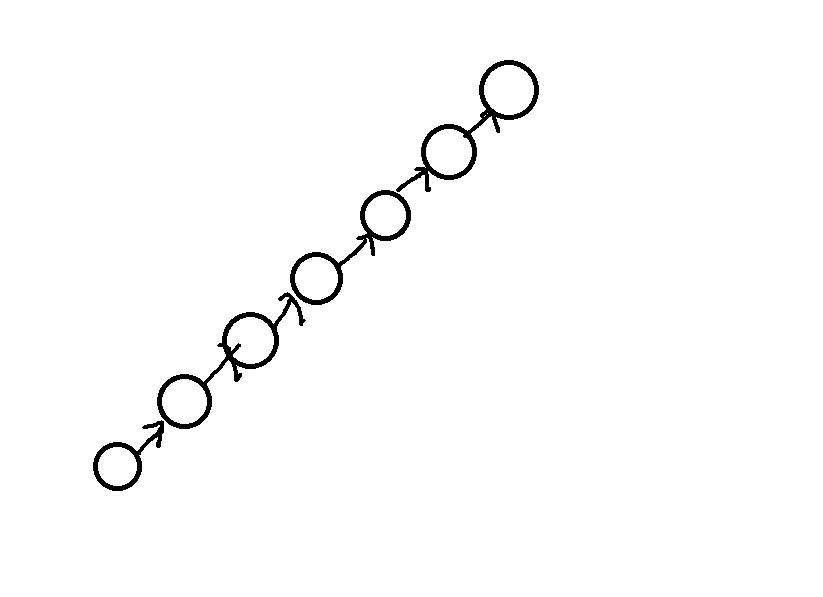
- 해결 방법
* rank를 이용한 union -> 트리를 편향되지 않게 만들자
1. 각 노드는 자신을 루트로 하는 subtree의 높이를 랭크rank라는 이름으로 저장한다.
2. 두 집합을 합칠 때 rank가 낮은 집합을 rank가 높은 집합에 붙인다.
* path compression
findSet을 행하는 과정에서 만나는 모든 노드들이 직접 root를 가리키도록 포인터를 바꾸어준다.
// Java program to implement Union-Find with union
// by rank and path compression
import java.util.*;
class GFG
{
static int MAX_VERTEX = 101;
// Arr to represent parent of index i
static int []Arr = new int[MAX_VERTEX];
// Size to represent the number of nodes
// in subgxrph rooted at index i
static int []size = new int[MAX_VERTEX];
// set parent of every node to itself and
// size of node to one
static void initialize(int n)
{
for (int i = 0; i <= n; i++)
{
Arr[i] = i;
size[i] = 1;
}
}
// Each time we follow a path, find function
// compresses it further until the path length
// is greater than or equal to 1.
static int find(int i)
{
// while we reach a node whose parent is
// equal to itself
while (Arr[i] != i)
{
Arr[i] = Arr[Arr[i]]; // Skip one level
i = Arr[i]; // Move to the new level
}
return i;
}
// A function that does union of two nodes x and y
// where xr is root node of x and yr is root node of y
static void _union(int xr, int yr)
{
if (size[xr] < size[yr]) // Make yr parent of xr
{
Arr[xr] = Arr[yr];
size[yr] += size[xr];
}
else // Make xr parent of yr
{
Arr[yr] = Arr[xr];
size[xr] += size[yr];
}
}
// The main function to check whether a given
// gxrph contains cycle or not
static int isCycle(Vector<Integer> adj[], int V)
{
// Itexrte through all edges of gxrph,
// find nodes connecting them.
// If root nodes of both are same,
// then there is cycle in gxrph.
for (int i = 0; i < V; i++)
{
for (int j = 0; j < adj[i].size(); j++)
{
int x = find(i); // find root of i
// find root of adj[i][j]
int y = find(adj[i].get(j));
if (x == y)
return 1; // If same parent
_union(x, y); // Make them connect
}
}
return 0;
}
// Driver Code
public static void main(String[] args)
{
int V = 3;
// Initialize the values for arxry Arr and Size
initialize(V);
/* Let us create following gxrph
0
| \
| \
1-----2 */
// Adjacency list for graph
Vector<Integer> []adj = new Vector[V];
for(int i = 0; i < V; i++)
adj[i] = new Vector<Integer>();
adj[0].add(1);
adj[0].add(2);
adj[1].add(2);
// call is_cycle to check if it contains cycle
if (isCycle(adj, V) == 1)
System.out.print("Graph contains Cycle.\n");
else
System.out.print("Graph does not contain Cycle.\n");
}
}
// This code is contributed by PrinciRaj1992
출처: 위키피디아 en.wikipedia.org/wiki/Disjoint-set_data_structure
Disjoint-set data structure - Wikipedia
MakeSet creates 8 singletons. After some operations of Union, some sets are grouped together. In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of
en.wikipedia.org
www.geeksforgeeks.org/union-find-algorithm-union-rank-find-optimized-path-compression/
'CS > algorithm' 카테고리의 다른 글
| MST(Minimum Spanning Tree): 최소 신장 트리 (0) | 2021.05.14 |
|---|---|
| 위상 정렬 (Topological Sorting) (0) | 2021.04.24 |
| Dijkstra Algorithm: 다익스트라 알고리즘 (0) | 2021.03.24 |
| Counting Sort: 계수 정렬 (0) | 2021.03.09 |
| Quick Sort: 퀵 정렬 (0) | 2021.03.07 |